深度学习常见问题汇总
深度学习常见问题汇总
深度学习与机器学习有什么区别
人工智能包含机器学习;机器学习包含深度学习
算法复杂度
可解释性;
数据需求
计算资源
特征的提取
决策边界(线性/非线性)
ANN(人工神经网络)的基本结构
单个感知机(或神经元)可以想象为逻辑回归。ANN可以视为一组多层感知机/神经元
ANN被称为前馈神经网络,因为输入只在正向处理
ANN结构由输入层,隐藏层,输出层构成
在分类任务中,我们通常在感知器的输出层中使用 Softmax 函数作为激活函数,以保证输出的是概率并且相加等于 1
单层感知机和MLP
单层感知器——这是最简单的前馈神经网络,不包含任何隐藏层
多层感知器——多层感知器有至少一个隐藏层
单层感知器只能学习线性函数,而多层感知器也可以学习非线性函数
激活函数的作用,常用的激活函数有哪些
为神经网络增强非线性变换,提高网络的特征提取能力和表达能力;
sigmoid;tanh;ReLU;softmax;
ReLU :可以有效解决梯度消失和梯度爆炸的问题(导数为 1);正则化作用(稀疏激活);
ReLU变体:防止部分神经元一直无法激活(“死亡”ReLUs问题)
前向传播和反向传播
前向传播目的:得到损失值
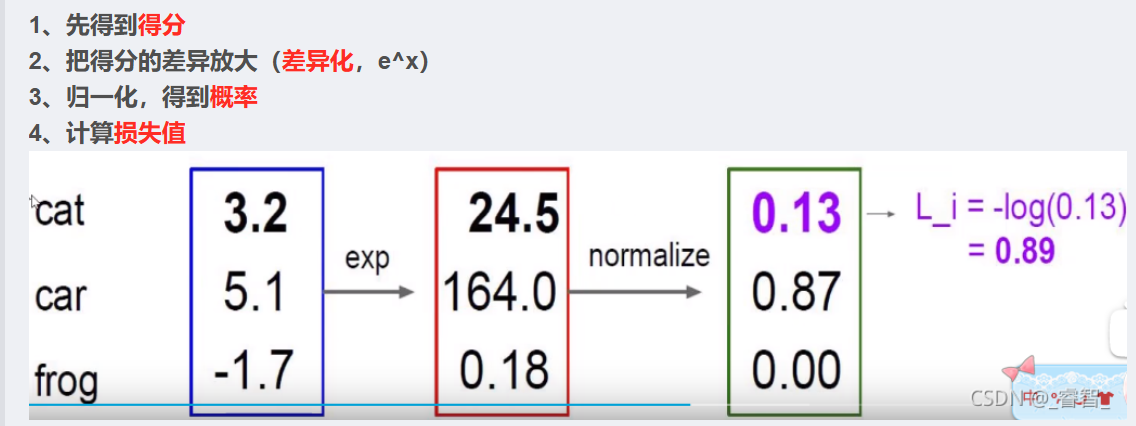
反向传播目的:为了让损失函数的值最小(利用梯度进行反向更新参数)
前向传播从输入到输出,逐层计算,目的是得到损失值;
反向传播则通过梯度下降,从输出往回层层求导,更新权重,以优化模型。
解释梯度下降算法在深度学习中的应用
梯度下降(Gradient Descent)是一种优化算法,用于寻找最小化损失函数(或成本函数)的参数值
损失函数衡量了模型预测值与真实值之间的差异,而梯度下降则是用于更新模型的参数(例如权重和偏置),以最小化这个差异。
梯度下降算法的步骤:
初始化参数:随机初始化模型的参数(例如权重和偏置)。
计算梯度:使用当前参数计算损失函数关于这些参数的梯度。梯度是一个向量,指示了损失函数在每个参数上的局部变化率。
更新参数:将每个参数沿着梯度的反方向移动一小步,步长由学习率控制。学习率是一个超参数,决定了参数更新的幅度。
重复迭代:重复步骤2和3,直到满足某个停止条件(例如达到最大迭代次数、损失函数值足够小或梯度足够小)。
BGD(批量梯度下降)、SGD(随机梯度下降)、MBGD(小批量梯度下降) 有何不同
下面是一个表格,总结了批量梯度下降(BGD)、随机梯度下降(SGD)和小批量梯度下降(MBGD)的主要特点:
| 特性 | 批量梯度下降 (BGD) | 随机梯度下降 (SGD) | 小批量梯度下降 (MBGD) |
|---|---|---|---|
| 梯度计算 | 使用全部训练数据 | 使用单个样本 | 使用一小批样本 |
| 内存需求 | 高 | 低 | 中等 |
| 计算成本 | 高 | 低 | 中等 |
| 收敛速度 | 慢 | 快(震荡可能较大) | 较快(通常比BGD快) |
| 梯度稳定性 | 最稳定 | 最不稳定 | 较稳定 |
| 适用场景 | 小数据集 | 大数据集、在线学习 | 大数据集(常用) |
| 收敛到全局最小值 | 可能性较高 | 可能性较低 | 可能性较高 |
| 调整参数 | 较少 | 需要调整学习率等 | 需要调整小批量大小 |
| 特点 | 梯度估计最准确 | 训练速度快,但可能震荡 | 计算效率和稳定性平衡 |