最小生成树算法
最小生成树算法
从具有n个节点的连通图中选择 n-1 条边,使得所组成的树的权值最小,即为最小生成树
即以最小的成本(边的权值)将图中所有节点链接到一起
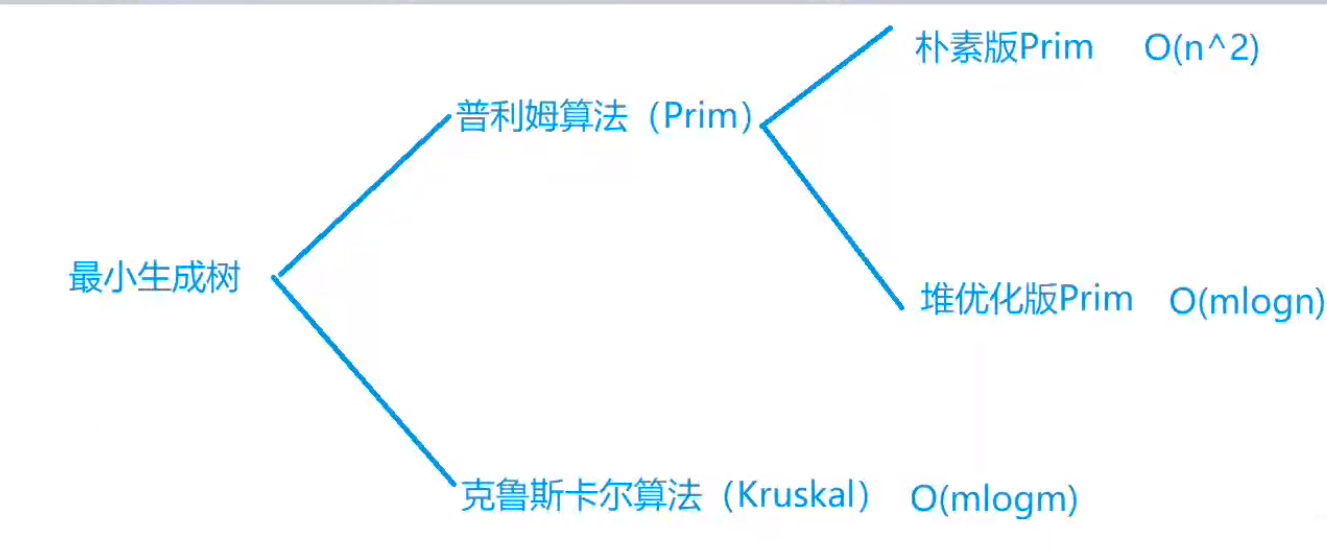
Prim
prim算法 是从节点的角度 采用贪心的策略 每次寻找距离 最小生成树最近的节点 并加入到最小生成树中
选节点 -> 加入 -> 更新其他点距离
- 循环n次,找到集合(最小生成树中的节点所组成)外距离最近集合最近的点t
- 点t加入集合
- 用 t 更新集合外其他点到集合的距离(到集合中任意一点的最小距离)
1 | |
堆优化版Prim
- 使用小根堆来判断 d数组 里的最小值
- 记录被确认的点的数量,当队列为空后,判断点数量是否与总节点数相同来判断是否有最小生成树
- 无向图的初始化:边数的两倍(
const int M = 2e5+10);add(a,b,w); add(b,a,w);
tips:
- M 数组来开小了,会超时
if(st[cur]) continue;必不可少的剪枝,防止超时 (不加会一直循环下去,如果非堆优化版本可以不加,因为它是通过n-1次的for循环来控制的)const int M = 3e5+10;//边数不够的话,也会报TLE , 无向图要开两倍(越大越好)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N = 510;
const int M = 2e5+10;
int h[N],e[M],ne[M],idx,w[M];
int n,m;
int d[N],st[N];
long long res;
priority_queue<PII,vector<PII>,greater<PII>> q;
void add(int u,int v,int value){
e[idx] = v; w[idx] = value; ne[idx] = h[u]; h[u] = idx++;
}
void dfs(int u){
for(int i=h[u];i!=-1;i=ne[i]){
int j = e[i];
if(!st[j] && w[i] < d[j]){
d[j] = w[i];
q.push({d[j],j});
}
}
}
int main(){
cin >> n >> m;
memset(h,-1,sizeof(h));
for(int i=0;i<m;i++){
int u,v,w;
cin >> u >> v >> w;
add(u,v,w); add(v,u,w);
}
memset(d,0x3f,sizeof(d));
memset(st,0,sizeof(st));
int cur = 1; //初始节点设置为1
d[1] = 0;
q.push({0,1});
// 我们只需要循环 n-1次,建立 n - 1条边,就可以把n个节点的图连在一起
while(q.size()){
int minv = 1e9; //每次选新节点前都要重新赋值
//1. 选节点
for(int j=1;j<=n;j++){
if(!st[j] && d[j] < minv){
minv = d[j];
cur = j;
}
}
//1.选节点
PII t = q.top();
cur = t.second;
q.pop();
if(st[cur]) continue; //必不可少的剪枝,防止超时
//2.加入最小生成树
st[cur] = 1;
//3. 更新距离
dfs(cur);
}
//d[1] 不用计算进来
for(int i=2;i<=n;i++){
if(d[i] > 10000){ //图中涉及边的边权的绝对值均不超过 10000
cout << "impossible";
return 0;
}
res += d[i];
}
cout << res;
return 0;
}
1 | |
Kruskal
kruscal的思路:
排序边 + 并查集
边的权值排序,因为要优先选最小的边加入到生成树里
遍历排序后的边
- 如果边首尾的两个节点在同一个集合,说明如果连上这条边图中会出现环
- 如果边首尾的两个节点不在同一个集合,加入到最小生成树,并把两个节点加入同一个集合
1 | |