注意力机制
注意力机制
注意力机制相关介绍链接
注意力机制的种类
聚焦式注意力和显著性注意力
- 聚焦式注意力:
- 显著性注意力:
通道注意力(Channel Attention),空间注意力(Spatial Attention),分支注意力(Branch Attention),自注意力(Self Attention)和交叉注意力(Cross Attention)
软注意力和硬注意力
软性注意力机制 可以理解为表示的是所有输入向量在注意力分布下的期望
而硬性注意力关注某一个输入向量。
硬注意力实现:选取最高概率的一个输入向量
硬注意力缺点: 最终的损失函数与注意力分布之间的函数关系不可导,不能反向传播来训练,需要使用强化学习训练。
注意力机制的计算
注意力机制的计算可以分为两步:
一是在所有输入信息上计算注意力分布
二是根据注意力分布来计算输入信息的加权平均
卷据、池化、全连接都是只考虑不随意线索
而注意力机制考虑随意线索。
- 随意线索被称为查询(query)
- 每个输入是一个值(value)和不随意线索(key)的对
- 通过注意力池化层(最大汇聚) 来有偏向性得选择某些输入
注意力就是从一堆线索中根据指定的规则挑选出需要的线索。类似于池化层去降维的感觉,可以节省计算资源。将注意力集中到有用的信息上,不要在噪声中花费时间

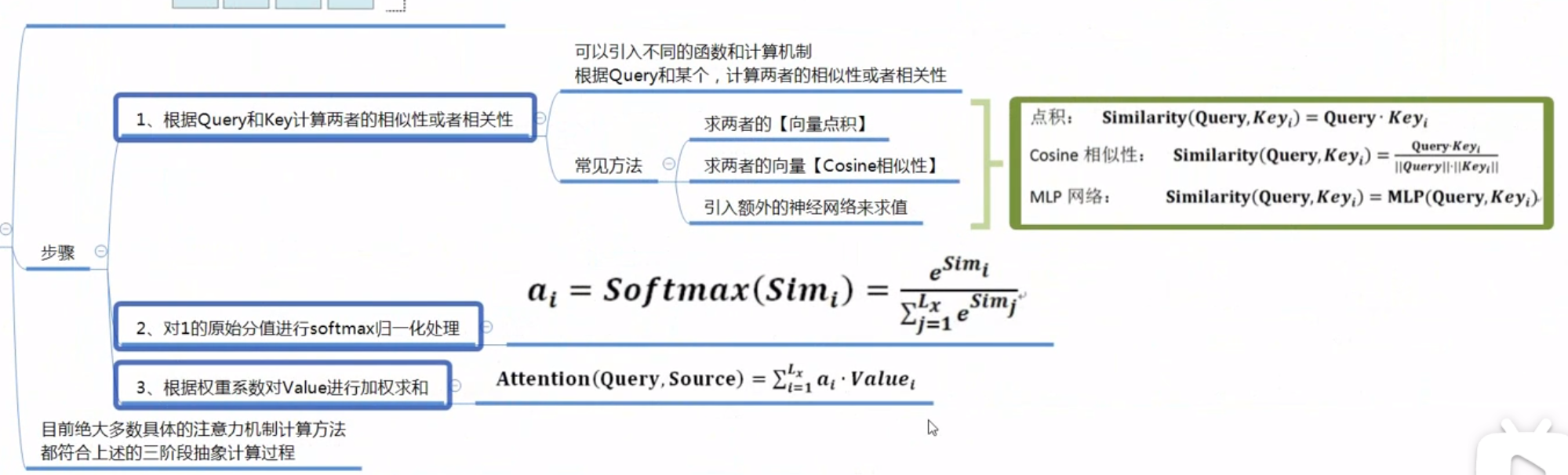
- 根据 queay 和 key 计算两者的相似性或者相关性
- 对1的原始分数进行 softmax 归一化处理
- 根据权重系数对 value 进行加权求和
$$
f(q) = \alpha(q,k_1)v_1 + \alpha(q,k_2)v_2 + \alpha(q,k_3)v_3 = \sum_{i=1}^3\alpha(q,k_i)v_i
$$
$\alpha(q,k_i) = softmax(a(q,k_i))$
注意力权重 = softmax(注意力分数)
注意力分数可以通过以下几种模型计算出来
vit中的自注意力机机制采用的就是缩放点积注意力模型
vision transformer中Attention是怎么计算的
Vision Transformer (ViT) 是一种将 Transformer 架构应用于图像分类任务的模型。Transformer 架构最初是为自然语言处理任务设计的,它的核心是自注意力(Self-Attention)机制,ViT 将这一机制扩展到了视觉领域。
在 Vision Transformer 中,图像首先被划分为多个小块(称为 Patch),然后这些小块被线性投影到一个固定维度的嵌入空间中。随后,这些嵌入被送入 Transformer 模型中进行处理。
Attention 机制的计算可以概括为以下几个步骤:
查询(Query)、键(Key)、值(Value)的计算:
- 对于输入的每个 Patch 嵌入,模型会分别计算其对应的查询(Q)、键(K)和值(V)。这通常通过三个不同的线性层实现。
注意力分数的计算:
- 使用查询(Q)和键(K)计算注意力分数。具体来说,对于每个查询,模型会计算它与所有键的相似度,这通常通过点积(dot product)来实现:
[ \text{Attention Score} = \frac{Q \cdot K^T}{\sqrt{d_k}} ]
其中,( Q ) 和 ( K ) 分别是查询和键的矩阵,( K^T ) 是 ( K ) 的转置,( d_k ) 是键的维度,分母中的 ( \sqrt{d_k} ) 是为了稳定训练过程中的梯度。
- 使用查询(Q)和键(K)计算注意力分数。具体来说,对于每个查询,模型会计算它与所有键的相似度,这通常通过点积(dot product)来实现:
Softmax 归一化:
- 计算得到的注意力分数通过 Softmax 函数进行归一化,使得所有分数的和为 1,这样可以得到每个查询对于每个值的注意力权重:
[ \text{Attention Weights} = \text{Softmax}(\text{Attention Score}) ]
- 计算得到的注意力分数通过 Softmax 函数进行归一化,使得所有分数的和为 1,这样可以得到每个查询对于每个值的注意力权重:
加权值(Value)的计算:
- 使用归一化的注意力权重对值(V)进行加权求和,得到最终的输出:
[ \text{Output} = \sum (\text{Attention Weights} \cdot V) ]
- 使用归一化的注意力权重对值(V)进行加权求和,得到最终的输出:
多头注意力(Multi-Head Attention):
- 在 Transformer 中,通常会使用多头注意力机制,即上述过程会被复制多次(头数),每个头学习到的是输入的不同表示。最后,所有头的输出会被合并起来,通常是通过拼接(concatenation)和再次线性变换来实现。
位置编码(Positional Encoding):
- 由于 Transformer 架构本身不具备捕捉序列顺序的能力,因此在 Vision Transformer 中,需要为图像的每个 Patch 添加位置编码,以提供位置信息。
层归一化(Layer Normalization)和残差连接(Residual Connection):
- 在每个注意力块之后,通常会使用层归一化和残差连接来促进深层网络的训练。
Vision Transformer 通过这种注意力机制能够捕捉图像中不同区域之间的关系,从而实现有效的图像表示学习。这种模型在多个视觉任务中展现出了与卷积神经网络(CNN)相比拟或更优的性能。
层归一化和残差连接的作用
层归一化(Layer Normalization)和残差连接(Residual Connection)是深度学习中两种常用的技术,它们在提高网络训练效率和性能方面起着重要作用,尤其是在深度网络中。
层归一化(Layer Normalization)
层归一化是一种归一化技术,旨在在网络的每一层对输入进行归一化处理。与传统的批量归一化(Batch Normalization)不同,层归一化是在单个数据样本的层面上进行归一化,而不是在整个批次上。
作用:
- 减少内部协变量偏移:层归一化通过规范化处理,减少了网络内部的协变量偏移问题,这有助于加速收敛速度。
- 提高模型稳定性:由于归一化减少了不同层间的尺度差异,这有助于网络训练过程中的稳定性。
- 允许更高的学习率:由于层归一化减少了梯度消失或爆炸的问题,因此可以使用更高的学习率进行训练。
- 简化网络初始化:归一化层使得网络对初始化不那么敏感,从而简化了网络的初始化过程。
残差连接(Residual Connection)
残差连接,也称为跳跃连接(Skip Connection),是一种允许网络中的信号绕过一层或多层直接传递的技术。
作用:
- 缓解梯度消失问题:在深层网络中,梯度可能会随着层数的增加而迅速减小,导致深层网络难以训练。残差连接通过直接连接层,帮助梯度直接流向前面的层,从而缓解了梯度消失问题。
- 提高模型容量:残差连接允许模型学习残差函数,这意味着模型可以学习到恒等映射(即直接传递输入到输出),这增加了模型的容量。
- 网络深度的扩展:残差连接使得可以训练更深的网络结构,因为它们减少了随着网络深度增加而性能下降的问题。
- 提高训练速度:残差连接有时可以加速模型的训练过程,因为它们允许网络更快地收敛。
在 Transformer 架构中的应用
在 Transformer 架构中,层归一化和残差连接被广泛使用:
- 层归一化通常应用于多头自注意力机制和前馈网络的输出上,以稳定训练过程并提高性能。
- 残差连接则被用于连接自注意力层和前馈网络的输入与输出,确保信息可以在网络中直接流动。
这两种技术的结合使得 Transformer 架构能够有效地处理长距离依赖问题,并在多种任务中取得了显著的性能提升。
为什么要使用缩放点积
点积之后方差为 $ d_k $
为什么在进行softmax之前需要对attention进行scaled
多头注意力计算
是的,多头注意力机制(Multi-Head Attention)在每个头内部独立进行注意力计算。这种机制是 Transformer 架构的关键组成部分,它允许模型同时从不同的表示子空间中捕获信息。
以下是多头注意力机制的一般步骤:
线性投影:输入序列首先被分割成查询(Query)、键(Key)和值(Value)三个部分,并且每个部分都通过独立的线性层(即一维卷积)进行投影,以生成不同头的输入。
分割为头:每个部分(Q、K、V)被分割成多个头,每个头处理输入序列的一部分信息。
并行处理:每个头独立地计算自注意力,即在每个头内,使用 Query 和 Key 计算注意力分数,然后这些分数用于加权 Value。
拼接头:所有头的输出被拼接在一起,形成一个较长的序列。
最终线性投影:拼接后的序列通过另一个线性层进行投影,以生成最终的输出。
在数学上,如果我们有 ( L ) 个头,每个头的注意力计算可以表示为:
[ \text{Attention}^l(Q, K, V) = \text{softmax}\left(\frac{QW^Q_l K^T W^K_l}{\sqrt{d_k}}\right) W^V_l V ]
[ \text{Output} = W^O \left[ \text{head}_1; \text{head}_2; …; \text{head}_L \right] ]
其中,( W^Q_l, W^K_l, W^V_l ) 是第 ( l ) 个头的线性层权重,( d_k ) 是 Key 的维度,( W^O ) 是最终输出的线性层权重。
多头注意力机制的主要优点
- 它能够使模型在不同的表示子空间中捕获信息,增强了模型的表达能力。
- 每个头可以学习到序列的不同方面,例如,一个头可能专注于捕捉短距离依赖,而另一个头可能专注于长距离依赖。最终,所有头的信息被整合,以获得全面的序列表示。