dp背包问题练习题
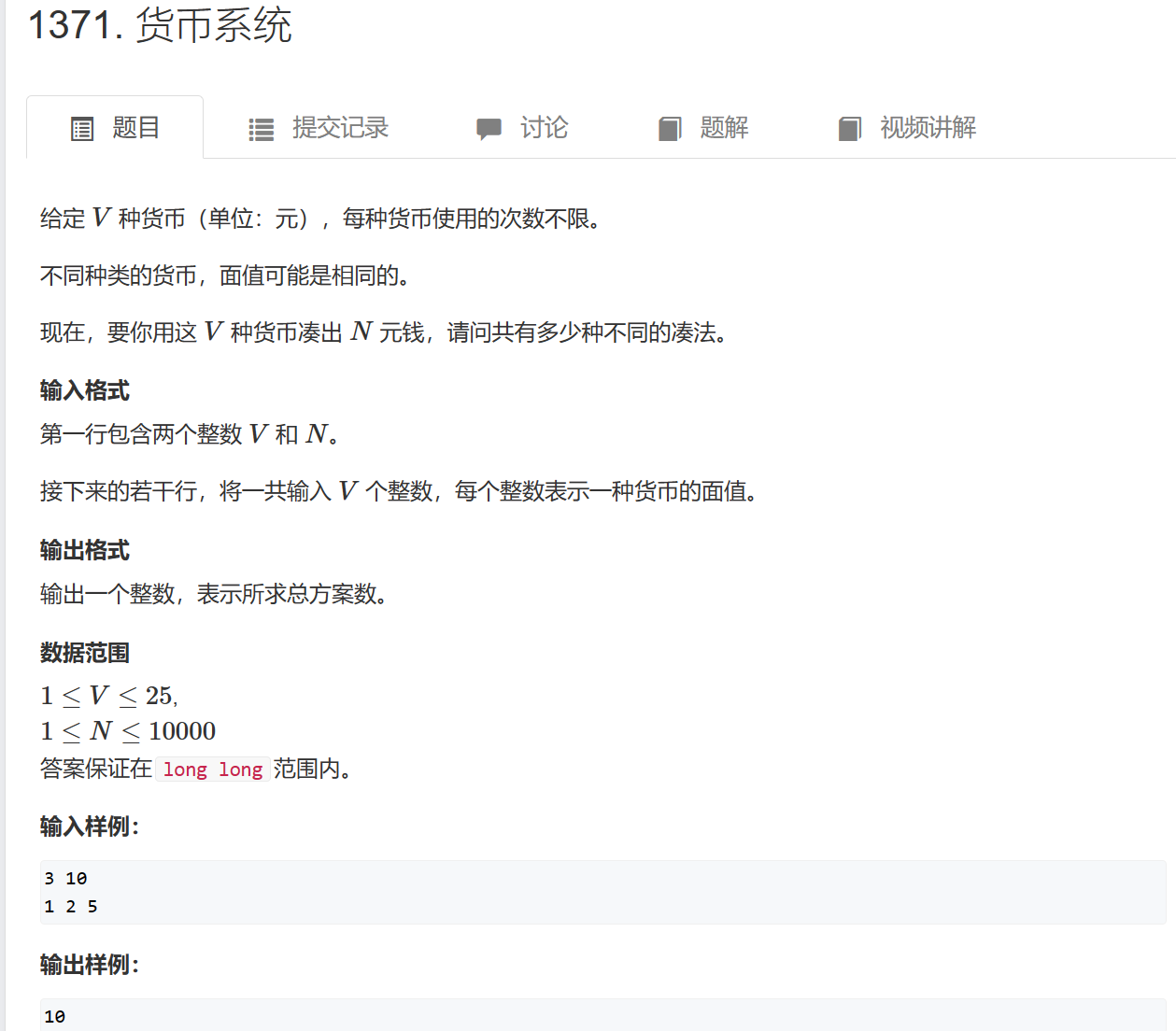
货币系统(完全背包)
tips:
- 要将$f[0][0]$ 等特殊的点进行初始化操作
- 要将$f[N][N] $设置为 $long long$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
typedef long long LL;
LL n,m;
LL v[N];
LL f[N][N];
int main(){
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i=1;i<=n;i++){
cin >> v[i];
}
f[0][0] = 1;
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
f[i][j] = f[i-1][j];
if(j >= v[i]) f[i][j] += f[i][j - v[i]];
}
}
cout << f[n][m];
}
|
包子凑数
问题简化为:输入n个数,求整数域内共有多少个数无法被这n个数通过加法来表示;
tips:
- 要将$f[0][0]$ 等特殊的点进行初始化操作
- 输入n个数,求整数域内共有多少个数无法被这n个数通过加法来表示;
- 当这n个数最大公因数等于 1 的时候,个数有限
- 最大公因数大于 1 的时候,个数无限
- 最大不能表示出来的数必定有个上界; 当两个数a,b(当gcd=1时),最大不能表示的数为(a-1)(b-1)-1 ; 当数字更多的时候,这个上界必然更小(可选的数字变多了); 而99和98是100内最大的互质的数,所以这个上界选择10000

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4+10;
int n,a[110],f[N][N];
int d;
int main(){
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n;
for(int i=1;i<=n;i++){
cin >> a[i];
d = gcd(d,a[i]);
}
f[0][0] = 1;
for(int i=1;i<=n;i++){
for(int j=0;j<=1e4;j++){
f[i][j] = f[i-1][j];
if(j >= a[i]) f[i][j] = max(f[i][j],f[i][j-a[i]]);
}
}
int cnt = 0;
for(int i=1;i<1e4;i++){
if(f[n][i] == 0) cnt++;
}
if(d > 1){
cout << "INF";
return 0;
}
cout << cnt;
return 0;
}
|
2022
从2022个物品中选择10个物品,并且物品总体积为2022的方案数

tips:
- 从 0到N 初始化 $f[i][0][0]$
1
2
3
| for(int i=0;i<=N;i++){
f[i][0][0] = 1;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| #include <iostream>
using namespace std;
const int N = 2030;
typedef long long LL;
LL f[N][15][N];
int main()
{
int a[N];
for(int i=0;i<=N;i++){
a[i] = i;
f[i][0][0] = 1;
}
for(int i=1;i<=2022;i++){
for(int j=1;j<=10;j++){
for(int k=1;k<=2022;k++){
f[i][j][k] = f[i-1][j][k];
if(k >= a[i]) f[i][j][k] += f[i-1][j-1][k-a[i]];
}
}
}
cout << f[2022][10][2022];
return 0;
}
|
砝码称重(0-1背包)
从前i个砝码中选,重量为 j 的方案数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
#include <iostream>
using namespace std;
const int N = 110;
const int M = 1e5+10;
int w[N];
int n,sum;
int f[N][2*M];
int main(){
cin >> n;
for(int i=1;i<=n;i++){
cin >> w[i];
sum+=w[i];
}
f[0][0] = 1;
for(int i=1;i<=n;i++){
for(int j=0;j<=sum;j++){
f[i][j] = f[i-1][j];
f[i][j] += f[i-1][abs(j-w[i])];
f[i][j] += f[i-1][j+w[i]];
}
}
int cnt=0;
for(int i=1;i<=sum;i++){
if(f[n][i]) cnt++;
}
cout << cnt;
return 0;
}
|
279. 完全平方数
279. 完全平方数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
int f[110][10010];
int numSquares(int n) {
memset(f,0x3f,sizeof(f));
f[0][0] = 0;
for(int i=1;i*i<=n;i++){
f[i][0] = 0;
for(int j=0;j<=n;j++){
f[i][j] = f[i-1][j];
if(j >= i*i) f[i][j] = min(f[i][j],f[i][j-i*i]+1);
}
}
int m = pow(n,1.0/2);
return f[m][n];
}
};
|
0-1背包练习题
一个大集合中要分出 两个集合
416. 分割等和子集
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如何正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
最后一块石头的重量 II
尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。



