线性dp练习题

数字三角形

题目链接：数字三角形

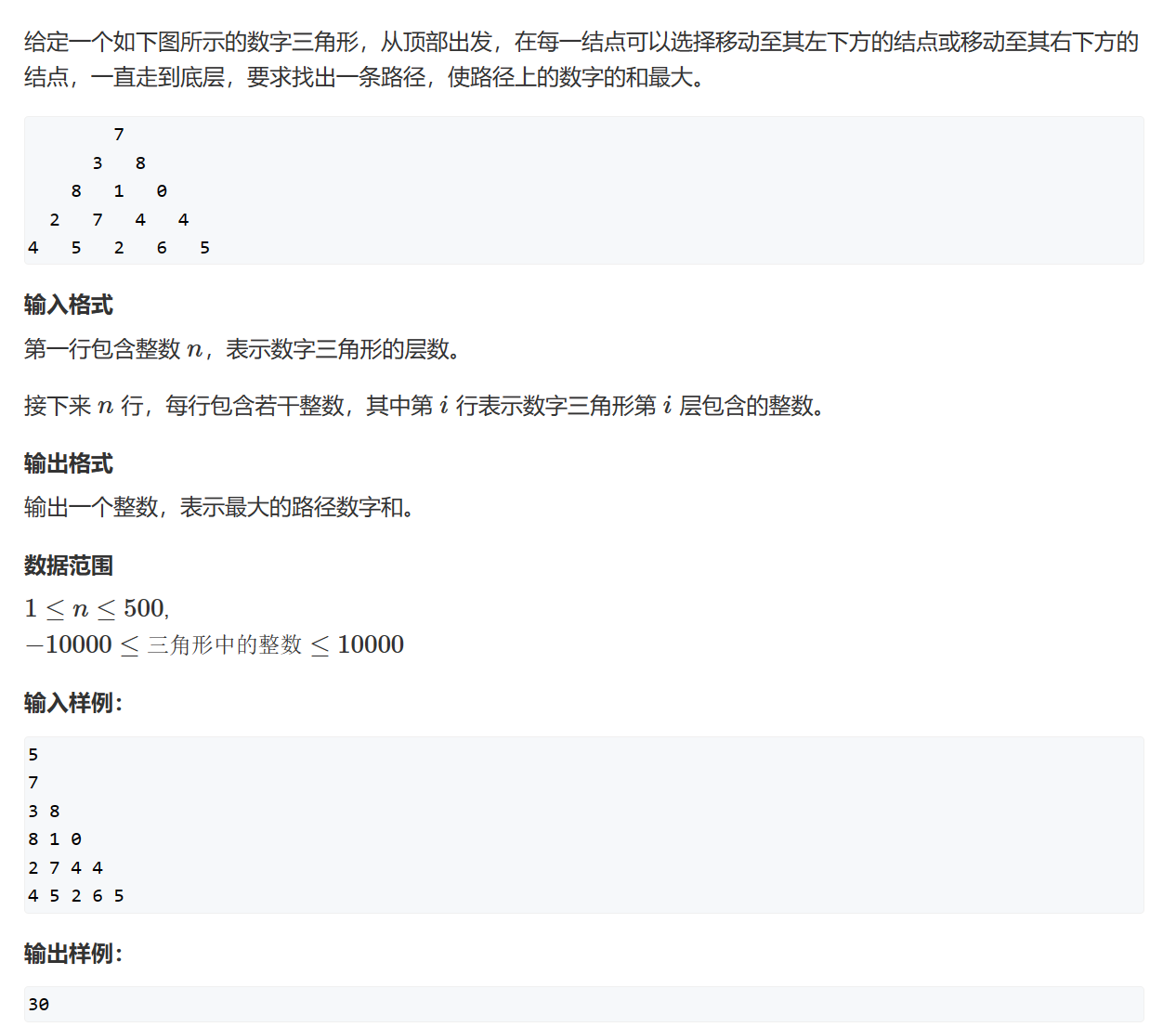
tips

1. 因为有些值为负数，因此要将所有$f[i][j]$初始为负无穷
   如果初始化为0会导致部分$f[i][j]$的值大于 本不应该大于 的f$f[i-1][j-1]$

#include <bits/stdc++.h>

using namespace std;

const int N = 510;

int n;
int a[N][N],f[N][N];

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin >> a[i][j];
        }
    }
    // 因为有些值为负数，因此要将所有f[i][j]初始为负无穷
    //如果初始化为0会导致部分f[i][j]的值大于 本不应该大于 的f[i-1][j-1]
    memset(f,-0x3f,sizeof(f));
    
    f[1][1] = a[1][1];
    
    for(int i=2;i<=n;i++){
        for(int j=1;j<=i;j++){
            f[i][j] = max(f[i-1][j] + a[i][j],f[i-1][j-1] + a[i][j]);
        }
    }
    int max_v = INT_MIN;
    for(int j=1;j<=n;j++){
        max_v = max(max_v,f[n][j]);
    }
    cout << max_v;
    return 0;
}

松散子序列

题目链接：松散子序列

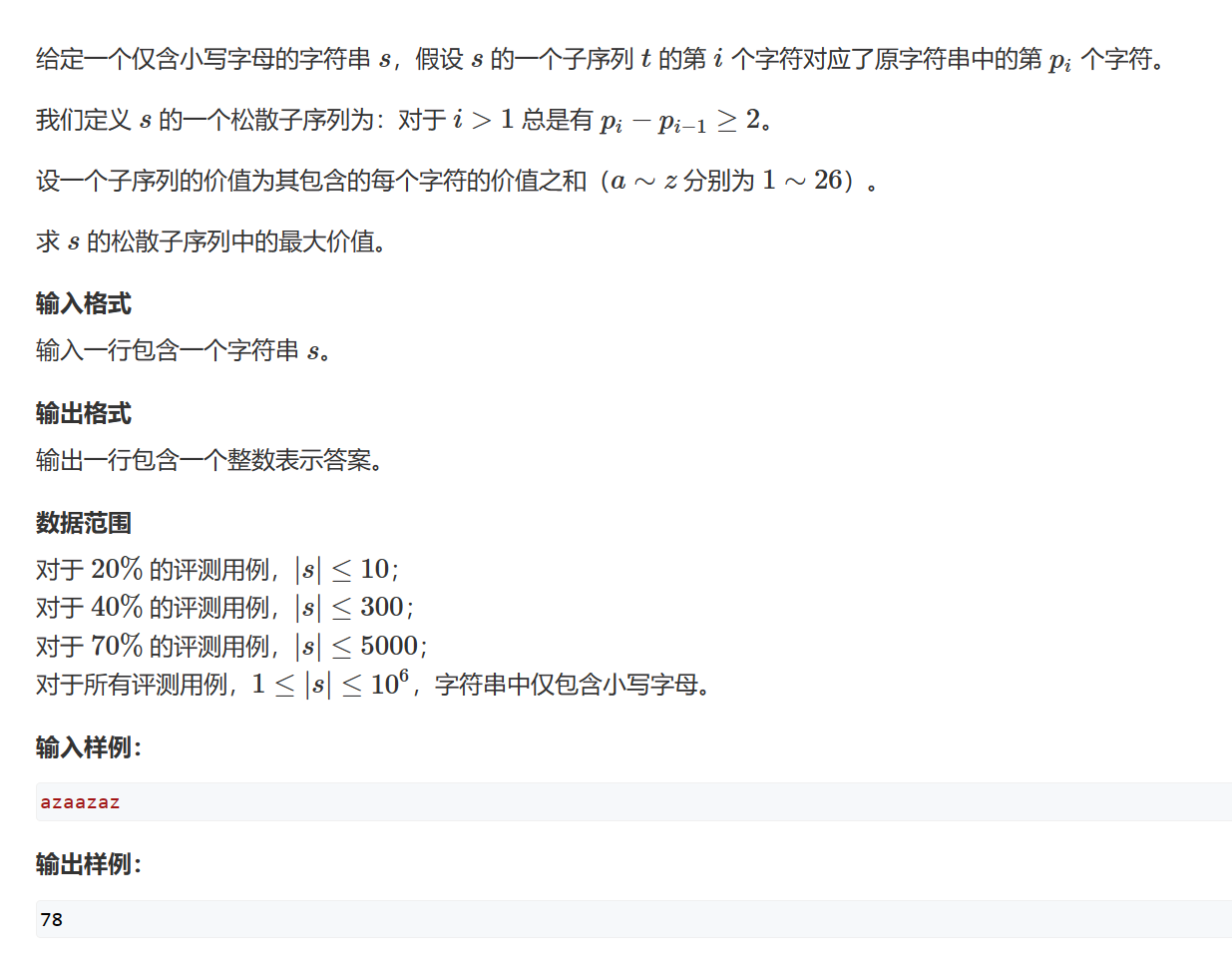
dp 思路：
以下标 $i$ (从1开始)结尾的松散子序列长度的最大值

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 10;

int f[N];
char s[N];
string str;

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> str;
    int n = str.size();
    for(int i=1;i<=n;i++){
        s[i] = str[i-1];
    }
    f[1] = s[1]-'a'+1;
    for(int i=1;i<=n;i++){
        if(i-1>=0) f[i] = max(f[i],f[i-1]);
        if(i-2>=0) f[i] = max(f[i],f[i-2] + s[i]-'a'+1);
    }
    // for(int i=1;i<=n;i++){
    //     cout << f[i] << "\n";
    // }
    cout << f[n];
    return 0;
}