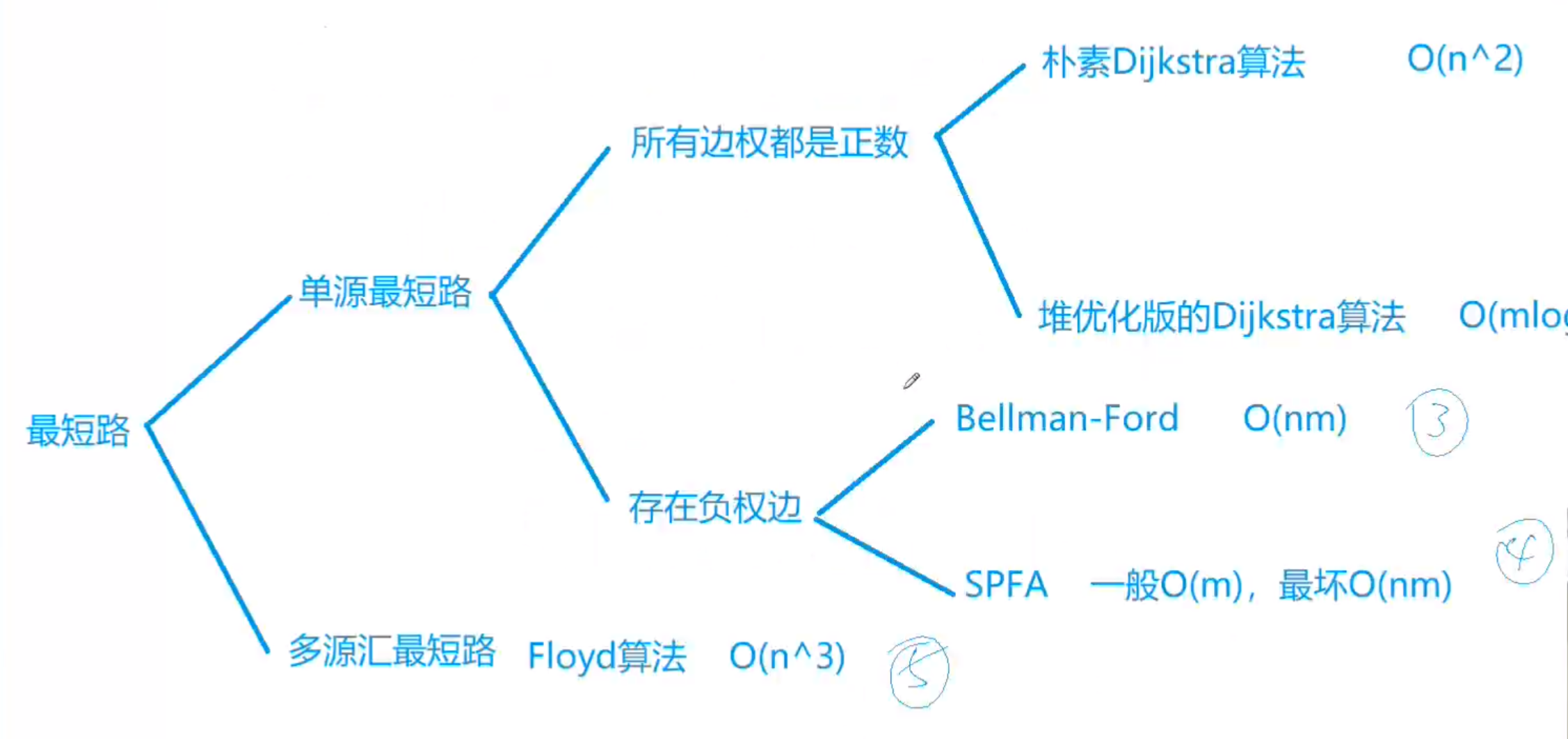
图的最短路问题

图的最短路问题

单源最短路

朴素Dijkstra算法

核心思想：

  1. 先确定最短距离点
  2. 然后用该点去更新其他点的最短距离

适合稠密图
变量：dist[N] （距离源点的距离数组） , st[N]（某个点是否已经被更新为距离最短的点的集合中的状态数组）
重边与自环：在min中会循环找出最短距离的边
算法步骤：

  1. 初始化：dist 初始化为正无穷（0x3f）memset(dist,0x3f,sizeof(dist)); st 初始化为0
  2. 更新已经得到最短距离的所有点所在集合；更新方法：遍历距离数组的所有点，将其中最小距离的点放入集合。
  3. 根据第二步最新得到那个点 t ，去更新其他点的最短距离
    d[j] = min(d[j],d[t] + t->j的距离)

Dijkstra求最短路图解

邻接矩阵版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510; //数据范围（最大输入节点数）

int n,m; // 节点/边数
int g[N][N]; // 图的邻接矩阵（稠密图用这个） ，算法复杂度为n^2
int dist[N]; //用于记录每一个点距离第一个点的距离
bool st[N]; //已经确定了最短路径的点为true

int dijkstra(){
    memset(dist,0x3f,sizeof(dist)); //将距离矩阵初始化为正无穷
    dist[1] = 0; // 题目要求 求出 1号点到 n号点的最短距离，第一个点到自身的距离为0
    
    for(int i=0;i<n;i++){   //有n个点所以要进行n次 迭代
    
        int t = -1;         //t存储着下方某轮次循环中找出的距离源点距离最近的点
        
        //找到路径最短的点：
        for(int j=1;j<=n;j++){  //此时的j代表从1号点开始,该处循环是找出此时距离源点距离最近的点
            if(!st[j] && (t==-1 || dist[t]>dist[j])){
                t = j;
            }
        }
        
        st[t] = true; //t的最短路径确定好了
        
        //对每个点的最短路径更新：
        //当有新的被确定最短路径的点加入到集合中时，
        //要对所有点（但实际只有剩余未被确定最短路径的点会被更新，因为最短路径的确定是由短到长的）距离源点的最短距离进行更新。
        for(int j=1;j<=n;j++){    //此处j<=n 必须要有等于号 //依次更新每个点所到相邻的点路径值
            if(!st[j]){     //跳过已经确定为最短路径的点
                dist[j]=min(dist[j],dist[t]+g[t][j]);
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}


int main(){
    cin >> n >> m;
    memset(g,0x3f,sizeof(g));//初始化图（邻接矩阵）
    while(m--){
        int a,b,c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b],c); //建图（邻接矩阵） ；当有重边时更新邻接矩阵中的权重为较小的那个权重。
    }
    
    int t = dijkstra();
    
    cout << t << endl;
    return 0;
}

邻接表版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <bits/stdc++.h>

using namespace std;

const int N = 510;
const int M = 1e5+10;

int n,m;
int h[N],e[M],ne[M],w[M],idx;
int d[N],st[N];
typedef pair<int, int> PII;//堆里存储距离和节点编号

void add(int a, int b, int v){
    e[idx] = b;
    w[idx] = v;
    ne[idx] = h[a];
    h[a] = idx++;
}

void dijkstra(){
    memset(d,0x3f,sizeof(d));
    d[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;//小根堆
    heap.push({0, 1});//插入距离和节点编号
    //遍历n次，每次找出一个点的最短距离
    for(int i=1;i<=n;i++){

        int t = -1; //需要被放入集合的点t

        //此时的j代表从1号点开始,该处循环是找出此时距离源点距离最近的点
        for(int j=1;j<=n;j++){
            if(!st[j] && (t == -1 || d[j] < d[t])){
                t = j;
            }
        }
        st[t] = 1;

        //更新未确定点的最短距离
        for(int k=h[t];k!=-1;k=ne[k]){
            int j = e[k];
            if(st[j]) continue; //如果该点已经被确定为了最短点集合中了就没必要再去更新它了
            d[j] = min(d[j],d[t] + w[k]);
        }
    }
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> n >> m;
    memset(h,-1,sizeof(h));
    while(m--){
        int a,b,v;
        cin >> a >> b >> v;
        add(a,b,v);
    }
    dijkstra(); //找出所有点到源点的距离
    if(d[n] == 0x3f3f3f3f) cout << "-1";
    else{
        cout << d[n];
    }
    return 0;
}

堆优化Dijkstra算法

适合稀疏图
使用小根堆：priority_queue<PII,vector<PII>,greater<PII>> heap

tips:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>

using namespace std;

const int N = 2*1e5;
const int M = 3*1e5+10;

int n,m;
int h[N],e[M],ne[M],w[M],idx;
int d[N],st[N];
typedef pair<int, int> PII;//堆里存储距离和节点编号

void add(int a, int b, int v){
    e[idx] = b;
    w[idx] = v;
    ne[idx] = h[a];
    h[a] = idx++;
}

void dijkstra(){
    memset(d,0x3f,sizeof(d));
    d[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;//小根堆
    heap.push({0, 1});//插入距离和节点编号
    //此处有while循环
    while(heap.size()){
        PII t = heap.top();
        //距离源点的距离dist，其节点编号为index
        int dist = t.first; int index = t.second;
        heap.pop();
        //如果该点已经被放入到最短路径集合中了的话就可以continue
        if(st[index]) continue; //必不可少的剪枝，防止超时
        st[index] = true;
            
        //更新index所指向的节点距离
        for(int k=h[index];k!=-1;k=ne[k]){
            int j = e[k];
            d[j] = min(d[j],dist + w[k]);
            heap.push({d[j],j});
        }
    }
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> n >> m;
    memset(h,-1,sizeof(h));
    while(m--){
        int a,b,v;
        cin >> a >> b >> v;
        add(a,b,v);
    }
    dijkstra(); //找出所有点到源点的距离
    if(d[n] == 0x3f3f3f3f) cout << "-1";
    else{
        cout << d[n];
    }
    return 0;
}

bellman-ford

思路：对 所有边 进行 n-1次松弛 操作

松弛：
遍历所有边，更新 边的终节点 到 起点 的最短距离
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value

为什么是n-1次操作：

第一次松弛 能得到与起点 一条边相连的节点的最短路径
第二次松弛 能得到与起点 两条边相连的节点的最短路径
……
第n-1次松弛 能得到与起点 n-1条边相连的节点的最短路径(n个节点，n-1条边即可相连)

判断是否有负权回路

在n-1次松弛的基础上，再多松弛一次，看minDist数组 是否发生变化。如果变化了就有负权回路

有边数限制的bellman-ford算法

要算从 1 号点到 n 号点的最多经过 k 条边的最短距离

bellman_ford 标准写法是松弛 n-1 次，此时就松弛 k 次就好

在最多经过 k 个城市的条件下，从城市 src 到城市 dst 的最低运输成本。此时是松弛 k+1 次（因为经过k个城市意味着会经过k+1条边）

要使用复制数组的关键在于两个因素：

  1. 图中可以有负权回路，说明只要多做松弛，结果是会变的。
  2. 要求最多经过k个节点，对松弛次数是有限制的。

以上两种情况需要使用复制数组

acwing流程:

  1. 初始化（结构体数组，d数组设置为无穷大）
  2. 循环k次（边数限制为k）
  3. 每次循环时，对所有的边进行更新操作（要先进行数组备份，使用备份的数组进行更新，防止出现串联操作从而导致实际最短路走过的长度大于k）
  4. 判断是否有路径（大于 0x3f3f3f3f / 2）即为无路径（起点和终点不连通，但终点和别的点连通）

有边数限制的最短路

适用于有负权边的最短路（有边数限制的最短路）

注意事项

  1. 有边数限制时，要注意防止一次松弛前进多步
1
2
3
4
5
6
7
8
9
10
//防止一次松弛前进多条边
memcpy(cpy,d,sizeof(d));

//遍历m条边
for(int i=0;i<m;i++){
    int a = u[i].a; int b = u[i].b; int w = u[i].w;
    if(cpy[a] + w < d[b]){
        d[b] = cpy[a] + w; //比较的时候用复制的数组，更新的时候才用原数组
    }
}
  1. 由于存在负权边，返回值长度可能恰好是 -1 的情况下会报错
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    int bellman_ford(){
        ...
        if(d[n] > 0x3f3f3f3f / 2) return -1; //不能这么写，因为有可能路径长度恰好是 -1
        else{
            return d[n];
        }
    }

    int main(){
        ...
        int res = bellman_ford();
        if(res == -1){
            cout << "impossible";
        }
        else{
            cout << res;
        }
        return 0;
    }

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <bits/stdc++.h>

using namespace std;

const int N = 1e4;
const int M = 1e5;

struct node{
    int a,b,w;    
}u[M];

int n,m,k;
int d[N],cpy[N];


void bellman(){
    memset(d,0x3f,sizeof(d));
    d[1] = 0;  //起点为节点1， 起点到起点的距离为0，所以 minDist[1] 初始化为0
    
    //k次松弛
    for(int i=0;i<k;i++){
        
        //防止一次松弛前进多条边
        memcpy(cpy,d,sizeof(d));
        
        //遍历m条边
        for(int j=0;j<m;i++){
            int a = u[j].a; int b = u[j].b; int w = u[j].w;
            if(cpy[a] + w < d[b]){
                d[b] = cpy[a] + w; //比较的时候用复制的数组，更新的时候才用原数组
            }
        }
    }
    
}

int main(){
    cin >> n >> m >> k;

    //先存储要进行遍历的边
    for(int i=0;i<m;i++){
        int a,b,v;
        cin >> a >> b >> v;
        u[i] = {a,b,v};
    }
    
    bellman();
    if(d[n] > 1e9) cout << "impossible"; //d[n]没被更新 代表 没有路径
    else{
        cout << d[n];
    }
    
    return 0;
}

spfa算法

dijkstra 和 spfa算法的区别
dijkstra是基于贪心的思想，每次选择最近的点去更新其它点，过后就不再访问。
而在spfa算法中，只要有某个点的距离被更新了，就把它加到队列中，去更新其它点，所有每个点有被重复加入队列的可能。

Floyd算法

动态规划思想

g[i][j] = min(g[i][j],g[i][k] + g[k][j]);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>
#include <cstring>

using namespace std;

const int N = 210;
int g[N][N];
int n,m,k;

void floyd(){
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                g[i][j] = min(g[i][j],g[i][k] + g[k][j]);
            }
        }
    }
}

int main(){
    cin >> n >> m >> k;
    memset(g,0x3f,sizeof(g));
    
    for(int i=0;i<m;i++){
        int x,y,z;
        cin >> x >> y >> z;
        
        //因为有重边，所以要用min取最小值
        g[x][y] = min(g[x][y],z);    
    }
/* 这三条边就是重边
3 4 5
3 4 6
3 4 7
*/
    floyd();
    
    while(k--){
        int x,y;
        cin >> x >> y;
        
        if(x == y){ //起点和终点相同是距离为0
            cout << 0 << "\n";
        }    
        else{
        
            if(g[x][y] > 1e9){
                cout << "impossible" << "\n";
            }
            else{
                cout << g[x][y] << "\n";
            }
        }
    }
    
    return 0;
}

多源最短路算法

算法 > 图论
#算法 #图论
图的最短路问题
https://cs-lb.github.io/2024/04/07/搜索与图论/图的最短路问题/
作者
Liu Bo
发布于
2024年4月7日
许可协议