线性dp

线性dp

线性DP，是较常见的一类动态规划问题，其是在线性结构上进行状态转移，这类问题不像背包问题、区间DP等有固定的模板

线性动态规划的目标函数为特定变量的线性函数，约束是这些变量的线性不等式或等式，目的是求目标函数的最大值或最小值

LCS问题——最长公共子序列

子序列 : 指的是字符串中不一定连续但先后顺序一致的n个字符
字符子串：指的是字符串中连续的n个字符
最长公共子序列，英文缩写为LCS（Longest Common Subsequence）。其定义是: 一个序列 S ，如果分别是两个或多个已知序列的子序列，且是所有符合此条件序列中最长的，则 S 称为已知序列的最长公共子序列。

问题描述：给定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。

状态表示

  1. 集合表示：所有 $ A[1,n] $和 $ B[1,m] $ 的公共子序列的集合
  2. dp[i][j]代表以s1[i]，s2[j]结尾的LCS的长度
  3. 属性：公共子序列长度的最大值

状态计算

  1. 找集合中所有情况的共同点和不同点来划分集合
  2. 该公共子序列分为四种情况：包括a[n] , b[m] ，不包括a[n] ,包括b[m] ，不包括a[n] , b[m] ，包括a[n] ,不包括b[m] （可以用二进制0 1来表示）
  3. $ f[i][j] $：A前i个字符，B前j个字符的公共子序列 的集合
    属性：maxlen
  4. 集合划分情况（假定）
    • (1) $ f[i-1][j-1] + 1 $ 同时包括 a[n] 和 b[m] （前提是a[n] == a[m]）
    • (2) $ f[i-1][j] $ 不包括a[n] ,包括b[m]
    • (3) $ f[i][j-1] $ 包括a[n] ,不包括b[m]
    • (4) $ f[i-1][j-1] $ a[n] 和 b[m] 都不包括
  5. 集合划分情况（实际）
    • f[i-1][j-1]+1 可以表示情况1 –> a
    • f[i][j-1]=max(情况2,情况4) –> b
    • f[i-1][j]=max(情况3,情况4) –> c
      所以我们最终只需要 求 max(a,b,c) 即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
\\最长公共子序列
#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

//注意题目中是字符
char a[N],b[N];  

int n,m,f[N][N];

int main(){
    cin >> n >> m;
	for(int i=1;i<=n;i++){
	    cin >> a[i];
	}
	for(int i=1;i<=m;i++){
	    cin >> b[i];
	}
	//状态计算
	for(int i=1;i<=n;i++){
	    for(int j=1;j<=m;j++){
            f[i][j] = max(f[i][j-1],f[i-1][j]);
            if(a[i] == b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
	    }
	}
    cout << f[n][m];
}

LIS问题——最长上升子序列

最长上升子序列（Longest Increasing Subsequence），简称LIS，也有些情况求的是最长非降序子序列，二者区别就是序列中是否可以有相等的数，对于固定的数组，虽然LIS序列不一定唯一，但LIS的长度是唯一的

  1. 状态设计：$dp[i]$ 代表以 $a[i]$ 结尾的LIS的长度

  2. 状态转移：$dp[i]=max{dp[j]+1，dp[i]} (1<=j< i，a[j]<a[i])$

  3. 边界处理：$dp[i]=1(1<=i<=n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int a[N],n;
int f[N]; //f[i]: 以 a[i] 为结尾的上升子序列的最大长度

int main(){
    int ans = 0;
    cin >> n;
    for(int i =1;i<=n;i++){
        cin >> a[i];
        f[i] = 1; //用1去初始化dp数组，因为最短的递增子序列的长度为1
    }
    //循环整个数组
    for(int i=1;i<=n;i++){
        //从前往后循环比那里之前的元素
        for(int j=1;j<=i-1;j++){
            if(a[j] < a[i]) f[i] = max(f[i],f[j]+1);
        }
        ans = max(ans,f[i]);
    }
    cout << ans;
    return 0;
}

求最长子序列的路径

核心思想：使用g数组存储序列中每个元素下标的上一个元素的下标
g[i] = j; : 最长子序列中下标为 i 的元素 的 上一个元素下标为 j

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e3+10;

int n,a[N],g[N],f[N]; 

int main(){
    cin >> n;
    for(int i=1;i<=n;i++){
        cin >> a[i];
    }
    for(int i=1;i<=n;i++){
        f[i] = 1;
        g[i] = 0;
        for(int j=1;j<=i-1;j++){
            if(a[i] > a[j]){
                f[i] = max(f[i],f[j]+1);
                //如果f[i]更新了，则说明最长子序列中 下标为i的元素的上一个元素下标为j
                if(f[i] == f[j]+1){
                    g[i] = j;
                }
            }
        }
    }
    int res = -1;
    int k; //最长子序列的最后一个元素的下标
    for(int i=1;i<=n;i++){
        if(f[i] > res){
            res = f[i];
            k = i;
        }
    }
    //res为最长子序列的长度
    for(int t=0;t<res;t++){
        cout << a[k] << " ";
        k = g[k]; //g[k]存储着 下标为k的元素 的上一个元素下标
    }
    // cout << res;
    return 0;
}

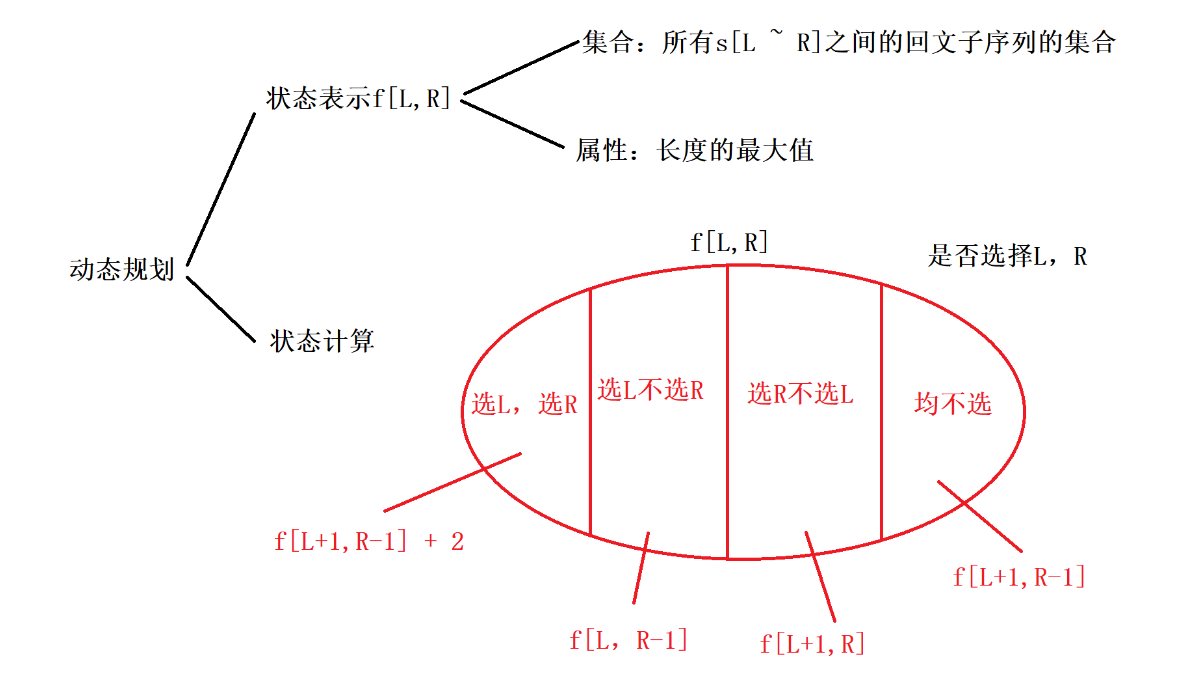
最长回文子序列

题目链接：密码脱落

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// f[i][j] 区间[i，j] 之间的最长 回文 子序列 长度
/* 
状态划分：
1. 字符 s[i]和s[j] 都在子序列中
2. 字符 s[i]在，s[j]不在
3. 字符 s[i]不在，s[j]在
4. 字符 s[i]和s[j] 都不在子序列中
*/
#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int f[N][N];
char s[N];

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> s;
    int n = strlen(s);
    for(int len=1;len<=n;len++){
        //r-l+1 = len
        for(int l=0; len+l-1 < n; l++){
            int r = len+l-1;
            if(len == 1){
                f[l][r] = 1;
                // continue;
            }
            else{
                f[l][r] = max(f[l][r-1],f[l+1][r]);
                if(s[l] == s[r]) f[l][r] = max(f[l][r],f[l+1][r-1] + 2);
            }
        }
    }
    cout << n - f[0][n-1];
    return 0;
}

得到具体的回文字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        if (n == 0) return "";
        
        // 初始化二维动态规划表
        bool f[n+1][n+1];

        // 填充对角线为true，因为单个字符总是回文
        for (int i = 0; i < n; ++i) {
            f[i][i] = true;
        }

        int start = 0, maxLen = 1; // 记录最长回文串的起始位置和长度

        // 填充动态规划表
        for (int len = 2; len <= n; ++len) { // 长度从2开始
            for (int i = 0; i + len - 1 < n; ++i) { // i是子串的起始位置,j是右端点小于n
                int j = i + len - 1; // j是子串的结束位置
                // 如果首尾字符相同，并且中间部分也是回文，则整个序列是回文
                if (s[i] == s[j] && (len < 3 || f[i + 1][j - 1])) {
                    f[i][j] = true;
                    maxLen = len;
                    start = i;
                }
                else {
                    f[i][j] = false;
                }
            }
        }

        // 返回最长的回文子串
        return s.substr(start, maxLen);
    }
};

算法 > 动态规划 > 线性dp
#算法 #动态规划 #线性dp
线性dp
https://cs-lb.github.io/2024/04/01/dp/线性dp/
作者
Liu Bo
发布于
2024年4月1日
许可协议